| (a) Show that if the response of an LTI system to
x(t) is the output y(t),
then the response of the system to
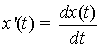
is y'(t). Do this problem in three
different ways:
(i) Directly from the
properties of linearity and time invariance and the
fact that:
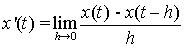
(ii) By differentiating the convolution
integral.
(iii) By examining the system in Figure 1.

(b) Demonstrate the validity of
the following relationships :-

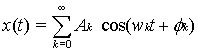
[Hint: These are easily done
using block diagrams as in (iii) of part (a) and the
fact that

(c) An LTI system has the response
y(t) = sinwot
to input x(t) = exp [-5t]
. u(t). Use the result of part (a)
to aid in determining the impulse response of
this system.
(d) Let s(t) be the
unit step response of a continuous-time LTI system.
Use part (b) to deduce that the
response y(t) to the input x(t)
is
 ( I )
( I )
Show also that
 ( II )
( II )
(e) Use equation ( I ) to determine the
response of an LTI system with step response
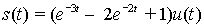
to the input x (t) = exp [t] . u (t).
(f) Let s[ n] be the unit step response
of a discrete - time LTI system. What are the discrete
- time counterparts of equations ( I ) and ( II )?
|